
깊이 우선 탐색 (DFS, Depth-First Search)
- DFS는 깊이 우선 탐색이라고 부르며 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
- 백트래킹에 사용하는 대표적인 탐색 알고리즘.
- 이진 트리 순회 알고리즘과 상당이 유사하다.
- BFS와 마찬가지로 어떤 정점을 방문했는지 반드시 기록한다.
⇒ 이렇게 하지 않으면 무한루프에 빠질 위험이 있다.
루트 노드 혹은 임의의 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식이다. 주로, 재귀함수 또는 Stack으로 구현할 수 있다.
- 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사.
- 넓게 탐색하기 전에 깊게 탐색.
탐색 방법

- 탐색 시작 노드를 스택에 삽입하고 방문 처리한다.
- 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
- 2번의 과정을 수행할 수 없을 때까지 반복.
장점
- 현재 경로상의 노드들만 기억하면 되므로 저장 공간의 수요가 비교적 적다.
- 목표 노드가 깊은 단계에 있는 경우 해를 빨리 구할 수 있다.
- BFS 보다 구현이 간단하다.
단점
- 단순 검색 속도가 BFS 보다 느리다.
- 해가 없는 경우에 빠질 수 있다. 즉, 사전에 탐색할 임의의 깊이를 지정할 필요가 있다.
- DFS는 해를 구하면 탐색이 종료된다. 따라서 구현 해가 최적의 해가 아닐 수 있다.
사용하는 경우
- 모든 노드를 방문 하고자 하는 경우
DFS 연습
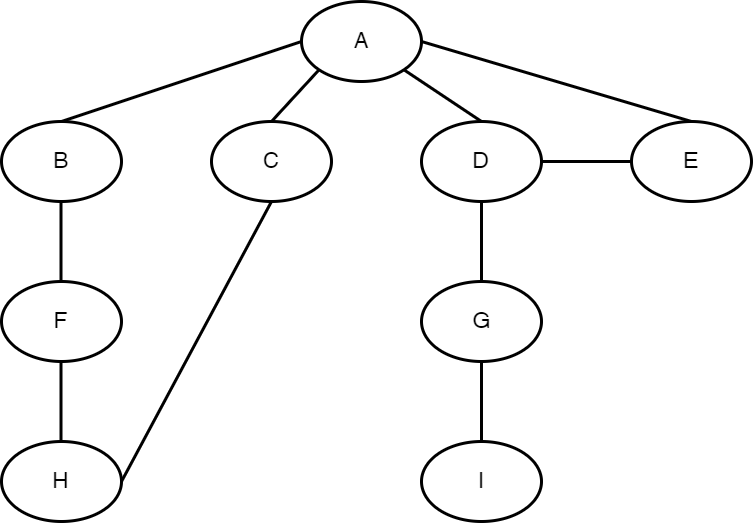
위 사진과 같은 그래프에서 깊이 우선 탐색 알고리즘을 실제로 수행한다.
- A부터 시작한다. A 정점에 방문했음을 표시한다.
- 이어서 A의 이웃을 순회한다. A의 이웃은 B, C, D, E다. 순서는 중요하지 않으니 B부터 시작한다.
- B에 깊이 우선 탐색을 수행한다.
- A에 깊이 우선 탐색을 수행하던 중이었으니 재귀 호출이다. A를 먼저 호출 스택에 추가한다.
- B가 현재 정점이 된다. B 정점에 방문했다고 표시한다.
- 이어서 B의 인접 정점인 A와 F를 순회한다.
- A는 이미 방문했으니 무시한다.
- 남은 인접 정점은 F 뿐이다. F에 깊이 우선 탐색 함수를 호출한다. B를 호출 스택에 추가한다. (A > B)
- F 정점에 방문했다고 표시한다.
- F의 인접 정점인 B와 H를 순회한다.
- B는 이미 방문했으니 무시한다.
- 남은 인접 정점은 H 뿐이다. H에 깊이 우선 탐색 함수를 호출한다. F를 호출 스택에 추가한다. (A > B > F)
- H 정점에 방문했다고 표시한다.
- H의 인접 정점인 F와 C를 순회한다.
- F는 이미 방문했으니 무시한다.
- C에 깊이 우선 탐색 함수를 호출한다. H를 호출 스택에 추가한다. (A > B > F > H)
- C 정점에 방문했다고 표시한다.
- C의 인접 정점인 H와 A를 순회한다.
- H는 이미 방문했으니 무시한다.
- A도 이미 방문했으니 무시한다.
- C에 다른 이웃이 없으니 C에 대한 깊이 우선 탐색은 여기서 끝이다. 호출 스택을 해제하기 시작한다.
- H를 팝한다. H에 남은 이웃이 없으니 H에 대한 깊이 우선 탐색이 끝났다.
- B를 팝한다. B 탐색도 끝났다.
- A를 팝한다. A의 이웃엔 아직 C, D, E가 남았다.
- C는 이미 방문했으니 무시한다.
- D에 깊이 우선 탐색 함수를 호출한다.
- D 정점에 방문했다고 표시한다.
- D의 인접 정점인 A, E, G를 순회한다.
- A는 이미 방문했으니 무시한다.
- E에 깊이 우선 탐색 함수를 호출한다. D를 호출 스택에 추가한다. (A > D)
- E 정점에 방문했다고 표시한다.
- E의 인접 정점인 A, D를 순회한다.
- A는 이미 방문했으니 무시한다.
- D도 이미 방문했으니 무시한다.
- E의 이웃을 모두 순회했고 E 탐색이 끝났다.
- 호출 스택에서 D를 팝해 D의 남은 이웃 G를 순회한다.
- G에 깊이 우선 탐색 함수를 호출한다. D를 호출 스택에 추가한다. (A > D)
- G 정점에 방문했다고 표시한다.
- G의 인접 정점인 D, I를 순회한다.
- D는 이미 방문했으니 무시한다.
- I에 깊이 우선 탐색 함수를 호출한다. G를 호출 스택에 추가한다. (A > D > G)
- I 정점에 방문했다고 표시한다.
- I의 인접 정점인 G를 순회한다.
- G는 이미 방문했으니 무시한다.
각 정점을 하나씩 팝하며 호출 스택을 해제한다. 호출 스택에 있던 각 정점마다 모든 이웃을 순회했으므로 컴퓨터가 더 할 일이 없다.
코드 구현
dfsTraverse(vertex, visitedVertices = new Map()) {
visitedVertices.set(vertex.value, true);
console.log(vertex.value);
for (let adjacentVertex of vertex.adjacentVertices) {
if (visitedVertices.get(adjacentVertex.value)) {
continue;
}
this.dfsTraverse(adjacentVertex, visitedVertices);
}
}
메서드는 vertex 하나와 선택적으로 visitedVertices 해시 테이블을 받는다. 함수를 처음 호출할 때 visitedVertices는 비어있지만 정점을 방문할 때마다 해시 테이블을 채우면서 각 재귀 호출에 해시 테이블을 전달한다.
가장 먼저 해시 테이블에 정점의 값을 추가하면서 정점을 방문했다는 표시를 남긴다.
이후 현재 정점의 인접 정점을 for문으로 순회한다.만일 이미 방문한 인접 정점이라면 다음 반복문으로 건너 뛴다.방문하지 않았다면 인접 정점에 dfsTraverse를 재귀적으로 호출한다.
깊이 우선 탐색을 사용해 실제 어떤 정점을 찾고 싶으면 함수를 다음과 같이 수정한다.
dfs(vertex, searchValue, visitedVertices = new Map()) {
// 찾고 있던 정점이면 원래의 vertex를 반환한다.
if (vertex.value === searchValue) {
return vertex;
}
visitedVertices.set(vertex.value, true);
console.log(vertex.value);
for (let adjacentVertex of vertex.adjacentVertices) {
if (visitedVertices.get(adjacentVertex.value)) {
continue;
}
// 인접 정점이 찾고 있던 정점이면 그 인접 정점을 반환한다.
if (adjacentVertex.value === searchValue) {
return adjacentVertex;
}
// 인접 정점에 계속해서 메서드를 재귀 호출해 찾고 있던 정점을 찾는다
const vertexWereSearchingFor = dfs(
adjacentVertex,
searchValue,
visitedVertices
);
// 찾았으면 그 정점을 리턴한다
if (vertexWereSearchingFor) {
return vertexWereSearchingFor;
}
}
// 찾고 있는 정점을 못 찾으면 null을 리턴한다.
return null;
}
- 재귀적으로 각 정점을 호출하되 원하는 정점을 찾으면 vertexWereSearchingFor을 리턴한다.
시간 복잡도
DFS는 그래프 (정점의 수 : N, 간선의 수 : E)의 모든 간선을 조회한다.
- 인접 리스트로 표현된 그래프 O(N+E)
- 인접 행렬로 표현된 그래프 O(N^2)
DFS를 활용하기 적합한 문제
- 경로의 특징을 저장해둬야 하는 문제 (경로 상의 노드를 기억해야 하는 문제)
- 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용
- 검색 대상 그래프 큰 문제
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다
프로그래머스 연습

Reference
[필수 알고리즘] DFS 깊이 우선 탐색 (Stack 구조) 이해
'자료구조' 카테고리의 다른 글
| [자료구조] 그래프(Graph) (0) | 2024.07.13 |
|---|---|
| [자료구조] 완전탐색 (Exhaustive search) (0) | 2024.04.14 |
| [자료구조] BFS(Breadth-First Search) (0) | 2024.03.31 |
| [자료구조] 정렬 (1) | 2024.03.25 |
| [자료구조] 스택과 큐 Stack vs Queue (2) | 2024.03.15 |
![[자료구조] DFS (Depth-First Search)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2Fdtnv55%2FbtsGBAFmjHt%2FAAAAAAAAAAAAAAAAAAAAAMar5yd2CWiUPnVR3nVqvZzoJQoTvG0DqvylVriUKGTL%2Fimg.png%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DuP8sZOV6XRXzoYADB9kxeuWhcR4%253D)